Time series forecasting is a crucial technique in finance, economics, weather prediction, and many other fields. It involves analyzing past data trends to make informed predictions about the future.

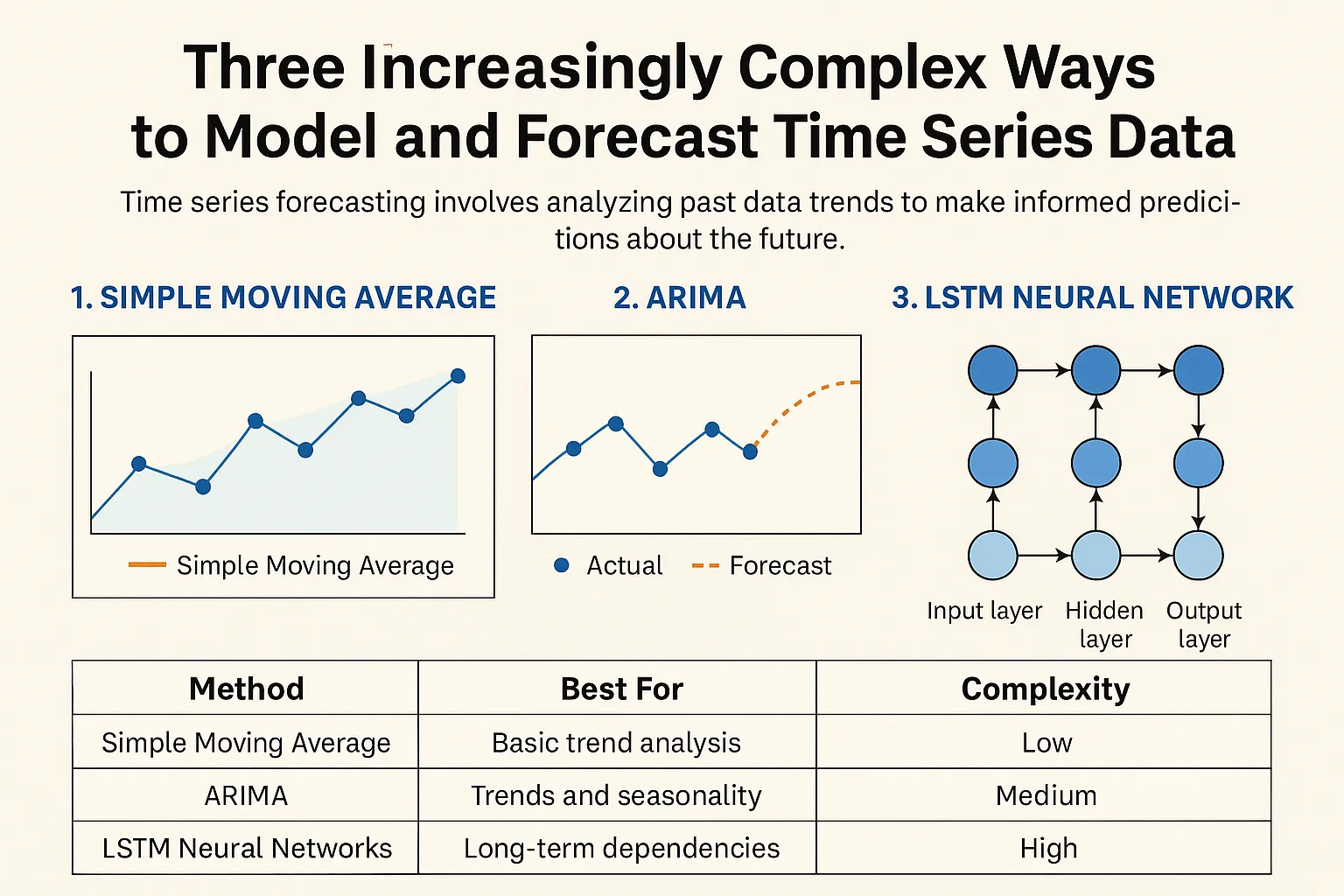
In this guide, we’ll explore three increasingly complex ways to model and forecast time series data, from simple statistical methods to advanced machine learning techniques.

Why Model Time Series Data?

Time series analysis helps businesses and researchers:

  • Detect trends: Identify patterns and long-term shifts.
  • Make predictions: Forecast future values based on historical data.
  • Optimize decision-making: Improve inventory management, stock trading, and demand forecasting.

Method 1: Simple Moving Averages (SMA)

The simplest way to model time series data is by using a moving average, which smooths out fluctuations and highlights trends.

Step 1: Install Required Libraries

Before implementing SMA, ensure you have the necessary Python libraries installed:

pip install numpy==1.21.6 pandas==1.3.5 matplotlib==3.5.2

Step 2: Calculate the Moving Average

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt

# Sample time series data
data = {'Date': pd.date_range(start='1/1/2023', periods=10, freq='D'),
        'Sales': [10, 12, 13, 15, 18, 20, 22, 24, 26, 30]}
df = pd.DataFrame(data)
df.set_index('Date', inplace=True)

# Calculate moving average
df['SMA_3'] = df['Sales'].rolling(window=3).mean()

# Plot results
df.plot(figsize=(10,5))
plt.title("Simple Moving Average")
plt.show()

Pros and Cons of SMA

  • Pros: Easy to implement, smooths fluctuations.
  • Cons: Lags behind actual values, not ideal for short-term forecasting.

Method 2: Autoregressive Integrated Moving Average (ARIMA)

ARIMA is a powerful statistical model that captures trends and seasonality in time series data.

Step 1: Install Required Libraries

Ensure the correct versions of the necessary libraries are installed:

pip install numpy==1.21.6 pandas==1.3.5 scipy==1.7.3 statsmodels==0.13.5 matplotlib==3.5.2 pmdarima==1.8.5

Step 2: Fit an ARIMA Model and Plot Results

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from pmdarima import auto_arima
from statsmodels.tsa.arima.model import ARIMA

# Sample time series data
data = {'Date': pd.date_range(start='1/1/2023', periods=10, freq='D'),
        'Sales': [10, 12, 13, 15, 18, 20, 22, 24, 26, 30]}
df = pd.DataFrame(data)
df.set_index('Date', inplace=True)

# Fit ARIMA model
model = auto_arima(df['Sales'], seasonal=False, trace=True)
best_order = model.order
arima_model = ARIMA(df['Sales'], order=best_order)
arima_fit = arima_model.fit()

# Forecast future values
forecast = arima_fit.forecast(steps=5)

# Plot the results
plt.figure(figsize=(10,5))
plt.plot(df.index, df['Sales'], label="Actual Sales", marker='o')
plt.plot(pd.date_range(df.index[-1], periods=6, freq='D')[1:], forecast, label="Forecast", linestyle='dashed', marker='o')
plt.legend()
plt.title("ARIMA Forecast")
plt.show()

Pros and Cons of ARIMA

  • Pros: Accounts for trends, more accurate than moving averages.
  • Cons: Requires stationarity, complex parameter tuning.

Method 3: Long Short-Term Memory (LSTM) Neural Networks

LSTMs are a type of deep learning model that excels in capturing complex patterns in sequential data.

Step 1: Install Required Libraries

pip install tensorflow==2.9.1 pandas==1.3.5 numpy==1.21.6 scikit-learn==1.0.2 matplotlib==3.5.2

Step 2: Define the Dataset

We will define the dataset again to ensure a standalone LSTM implementation.

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from sklearn.preprocessing import MinMaxScaler
import tensorflow as tf

# Sample time series data
data = {'Date': pd.date_range(start='1/1/2023', periods=20, freq='D'),
        'Sales': [10, 12, 13, 15, 18, 20, 22, 24, 26, 30, 32, 35, 38, 40, 42, 45, 47, 50, 52, 55]}
df = pd.DataFrame(data)
df.set_index('Date', inplace=True)

# Normalize data
scaler = MinMaxScaler()
df['Sales_scaled'] = scaler.fit_transform(df[['Sales']])

Step 3: Prepare Data for LSTM

# Create sequences for LSTM
def create_sequences(data, seq_length=5):
    X, y = [], []
    for i in range(len(data) - seq_length):
        X.append(data[i:i+seq_length])
        y.append(data[i+seq_length])
    return np.array(X), np.array(y)

sequence_length = 5
X, y = create_sequences(df['Sales_scaled'].values, seq_length=sequence_length)
X = np.expand_dims(X, axis=2)  # Reshape for LSTM input

Step 4: Build and Train the LSTM Model

# Define the LSTM model
model = tf.keras.Sequential([
    tf.keras.layers.LSTM(50, return_sequences=True, input_shape=(sequence_length, 1)),
    tf.keras.layers.LSTM(50),
    tf.keras.layers.Dense(1)
])

# Compile the model
model.compile(optimizer='adam', loss='mse')

# Train the model
model.fit(X, y, epochs=50, batch_size=1)

Step 5: Make Predictions and Plot Results

# Generate predictions
predicted_sales = model.predict(X)

# Transform back to original scale
predicted_sales = scaler.inverse_transform(predicted_sales)

# Plot the results
plt.figure(figsize=(10,5))
plt.plot(df.index[sequence_length:], df['Sales'].values[sequence_length:], label="Actual Sales", marker='o')
plt.plot(df.index[sequence_length:], predicted_sales, label="LSTM Predictions", linestyle='dashed', marker='o')
plt.legend()
plt.title("LSTM Forecast vs Actual Sales")
plt.show()

Pros and Cons of LSTM

  • Pros: Handles complex patterns, effective for long-term forecasting.
  • Cons: Requires large datasets and high computation power.

Comparison of Methods

Method Best For Complexity
Simple Moving Average Basic trend analysis Low
ARIMA Time series with trends and seasonality Medium
LSTM Neural Networks Complex, long-term forecasting High

Conclusion

Choosing the right method for time series forecasting depends on the dataset size, complexity, and accuracy requirements. Simple Moving Averages work for basic trends, ARIMA is ideal for structured patterns, and LSTMs excel at complex forecasts.

Experiment with these methods and find the best fit for your project!